Колонка Тейлора
Материал из OceanWiki.

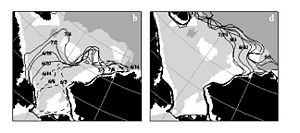
Колонка Тейлора (анг Taylor Column) Давайте для начала представим себе цилиндр (или в принципе любой другой маленький объект), который мы двигаем по дну покоящейся жидкости или который неподвижен в стационарном потоке. «Маленький» означает, что размеры его малы по сравнению с глубиной жидкости. Наша интуиция подсказывает нам, что такой объект должен создавать возмущения (гравитационные волны) в потоке, которые будут распространяться во всех направлениях. И это явление будет действительно иметь место при движении жидкости без вращения. Во вращающейся же жидкости будет происходить образование так называемой колонки Тейлора, т.е. во вращающейся жидкости подводный объект (в частности наш цилиндр) будет служить причиной отсутствия потока со ВСЕЙ водной толще непосредственно над объектом. Т.е. наш маленький цилиндрик будет вести себя так, как будто мы его растянули параллельно оси вращения до поверхности воды и опустили в жидкость. Это явление было впервые продемонстрировано Тейлором в его экспериментах в 1923 г. Его выводы используются для изучения влияния топографии подстилающей поверхности на потоки в атмосфере и в океане. Например, горы продуцируют так называемые «колонные» возмущения в воздухе, которые интерферируют или просто блокируют воздушные потоки на значительной высоте (однако же не во всей атмосфере!!!)
[править] Подробности
Ну а теперь немного математики, для тех кто сильно любопытен. Теорема, описывающая это явление, носит название Теоремы Тейлора –Праудмана, хотя на самом деле ее вывел Праудман в одиночестве (или о всяком случае без Тейлора) в 1915. Начинаем как всегда с уравнения Навье-Стокса и уравнения неразрывности. Уравнение Навье-Стокса:
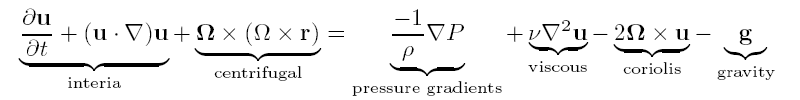 (1)
(1)
для жидкости плотности ρ, вращающейся с угловой скоростью Ω= (0; 0; ω) в поле силы тяжести g = (0; 0;-g), ν - кинематическая вязкость жидкости, u=(u,v,w) - вектор скорости, r- вектор положения
Уравнение неразрывности:
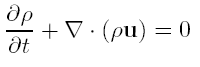 (2)
(2)
Мы можем упростить уравнение движения, если вспомним о том, что сила тяжести – потенциальная (консервативная) сила и может быть записана через градиент потенциала g=∇Φ.
Центробежная сила также может быть записана через градиент:
![]()
Тогда мы можем сгруппировать силу тяжести и центробежную силу в один член:
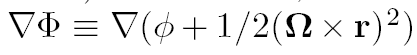 (3)
(3)
Прежде всего мы будем рассматривать потоки, для которых:
- число Рейнольдса велико (число Рейнольдса Re – это отношение сил инерции к силам вязкости)
- число Россби много меньше 1 (число Россби Rо – это отношение сил инерции к силе Кориолиса).
- Жидкость несжимаемая (т.е. плотность жидкости постоянна)
Таким образом, в уравнении движения мы можем пренебречь вязкостью и силами инерции
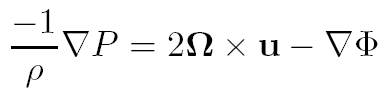 (4)
(4)
Т.е. мы получим то самое уравнение геострофического баланса (если кто не узнал=)). Теперь возьмем ротор от обеих частей равенства:
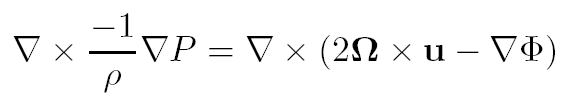 (5)
(5)
Для несжимаемой жидкости левая часть уравнения (5) вырождается (ротор градиента всегда равен 0). Если Ω постоянная, то правая часть уравнения (5) будет:
![]() (6)
(6)
!!! Напоминалка из векторной алгебры:
![]()
Для несжимаемой жидкости уравнение неразрывности имеет вид:
![]() (7)
(7)
и значит первый член правой части (6) также вырождается.
В результате уравнение (5) примет вид:
![]()
Так как Ω= (0; 0; ω), то
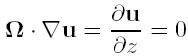
Таким образом, скорость жидкости в плоскости, параллельной оси вращения должна быть постоянной. А значит над подводным препятствие жидкость будет находиться в покое во всей колонке воды от поверхности препятствия до поверхности воды.
На самом деле это теорема говорит о большем, а именно, что трехмерное движение вращающейся, однородной, невязкой жидкости может быть без потерь представлено, как двумерное.
Источники:
http://ace.acadiau.ca/math/karsten/Projectwebpages/TimandJeff/fluid.pdf
http://www-paoc.mit.edu/12307/reports/tcolumns.pdf
http://seas.harvard.edu/brenner/taylor/physic_today/taylor.htm
Ссылки:
http://ace.acadiau.ca/math/karsten/Projectwebpages/TimandJeff/
Категория: Физическая океанология
